Bài viết về Lý thuyết Bất phương trình bậc nhất hai ẩn dành cho lớp 10 rất thú vị và chi tiết, giúp bạn hiểu rõ những kiến thức cốt lõi liên quan đến chủ đề này. Hãy cùng khám phá để nắm vững lý thuyết nhé!
Lý thuyết Bất phương trình bậc nhất hai ẩn
I. BẤT PHƯƠNG TRÌNH BẬC NHẤT VỚI HAI ẨN
Bất phương trình bậc nhất hai ẩn x và y có dạng tổng quát như sau:
ax + by ≤ c (1)
(có thể là ax + by < c; ax + by ≥ c; hoặc ax + by > c)
Trong đó, a, b, c là các số thực đã được xác định, và a cùng b không thể đồng thời bằng 0. x và y là các biến số cần tìm.
II. BIỂU DIỄN TẬP NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Giống như bất phương trình bậc nhất với một ẩn, bất phương trình bậc nhất với hai ẩn thường có vô số nghiệm. Để mô tả tập nghiệm của chúng, ta sẽ sử dụng phương pháp biểu diễn hình học.
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của bất phương trình (1) được gọi là miền nghiệm.
Dưới đây là quy trình để biểu diễn hình học tập nghiệm (hay miền nghiệm) của bất phương trình ax + by ≤ c (tương tự cho bất phương trình ax + by ≥ c):
Bước 1: Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng Δ: ax + by = c.
Bước 2: Chọn một điểm M0(x0; y0) không nằm trên Δ (thường chọn gốc tọa độ).
Bước 3: Tính giá trị ax0 + by0 và so sánh với c.
Bước 4: Kết luận
- Nếu ax0 + by0 < c thì nửa mặt phẳng bên chứa M0 là miền nghiệm của ax + by ≤ c.
- Nếu ax0 + by0 > c thì nửa mặt phẳng không chứa M0 là miền nghiệm của ax + by ≤ c.
Lưu ý: Miền nghiệm của bất phương trình ax + by ≤ c không bao gồm đường thẳng ax + by = c, trong khi miền nghiệm của bất phương trình ax + by < c lại không bao gồm đường thẳng này.
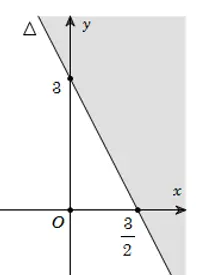
Ví dụ: Biểu diễn hình học tập nghiệm của bất phương trình 2x + y ≤ 3.
Giải:
Vẽ đường thẳng Δ: 2x + y = 3.
Chọn gốc tọa độ O(0;0), ta thấy O không thuộc Δ và có 2*0 + 0 < 3, do đó nửa mặt phẳng bên chứa gốc tọa độ O chính là miền nghiệm của bất phương trình đã cho (miền không được tô đậm trong hình).
III – HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Tương tự như hệ bất phương trình với một ẩn…Hệ bất phương trình bậc nhất hai ẩn là tập hợp của một số bất phương trình liên quan đến hai biến x và y, và nhiệm vụ của chúng ta là tìm ra các nghiệm chung cho chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho.
Tương tự như bất phương trình bậc nhất hai ẩn, chúng ta cũng có thể thể hiện hình học của tập nghiệm trong hệ bất phương trình này.
Ví dụ 2: Hãy biểu diễn hình học tập nghiệm của hệ bất phương trình dưới đây:
Giải thích:
Đầu tiên, chúng ta sẽ vẽ các đường thẳng sau:
- d1: 3x + y = 6
- d2: x + y = 4
- d3: x = 0 (trục Oy)
- d4: y = 0 (trục Ox)
Chúng ta nhận thấy rằng điểm M0 (1;1) có tọa độ thỏa mãn tất cả các bất phương trình trong hệ trên. Do đó, chúng ta sẽ tô đậm các nửa mặt phẳng bên cạnh (d1), (d2), (d3), (d4) không chứa điểm M0. Khu vực không được tô đậm (hình tứ giác OCIA cùng với bốn cạnh AI, IC, CO, OA trong hình vẽ) chính là miền nghiệm của hệ đã cho.
IV. ỨNG DỤNG TRONG BÀI TOÁN KINH TẾ
Việc giải quyết một số bài toán kinh tế thường dẫn đến việc xem xét các hệ bất phương trình bậc nhất hai ẩn và tìm cách giải quyết chúng. Loại bài toán này thuộc về một lĩnh vực toán học được gọi là Quy hoạch tuyến tính.
